Welcome! And thank you for taking an interest in my personal page.

Since joining the project as a PhD student in September 2019, I have focused on the description of waves and instabilities in three models: magnetohydrodynamics (MHD), Hall-magnetohydrodynamics (HMHD), and the ion-electron, two-fluid model. My projects include:
- an analytic analysis of waves in the two-fluid formalism with a focus on phase and group speed diagrams, as well as whistling behaviour.
- co-development of the Legolas code with a focus on implementing additional physics, particularly viscosity and the Hall current.
- a parametric study of the influence of background flow on the resistive tearing instability with Legolas.
Want to have a look at my work, or get in touch? Check out my personal page, ORCID record, and/or GitHub profile for more details.
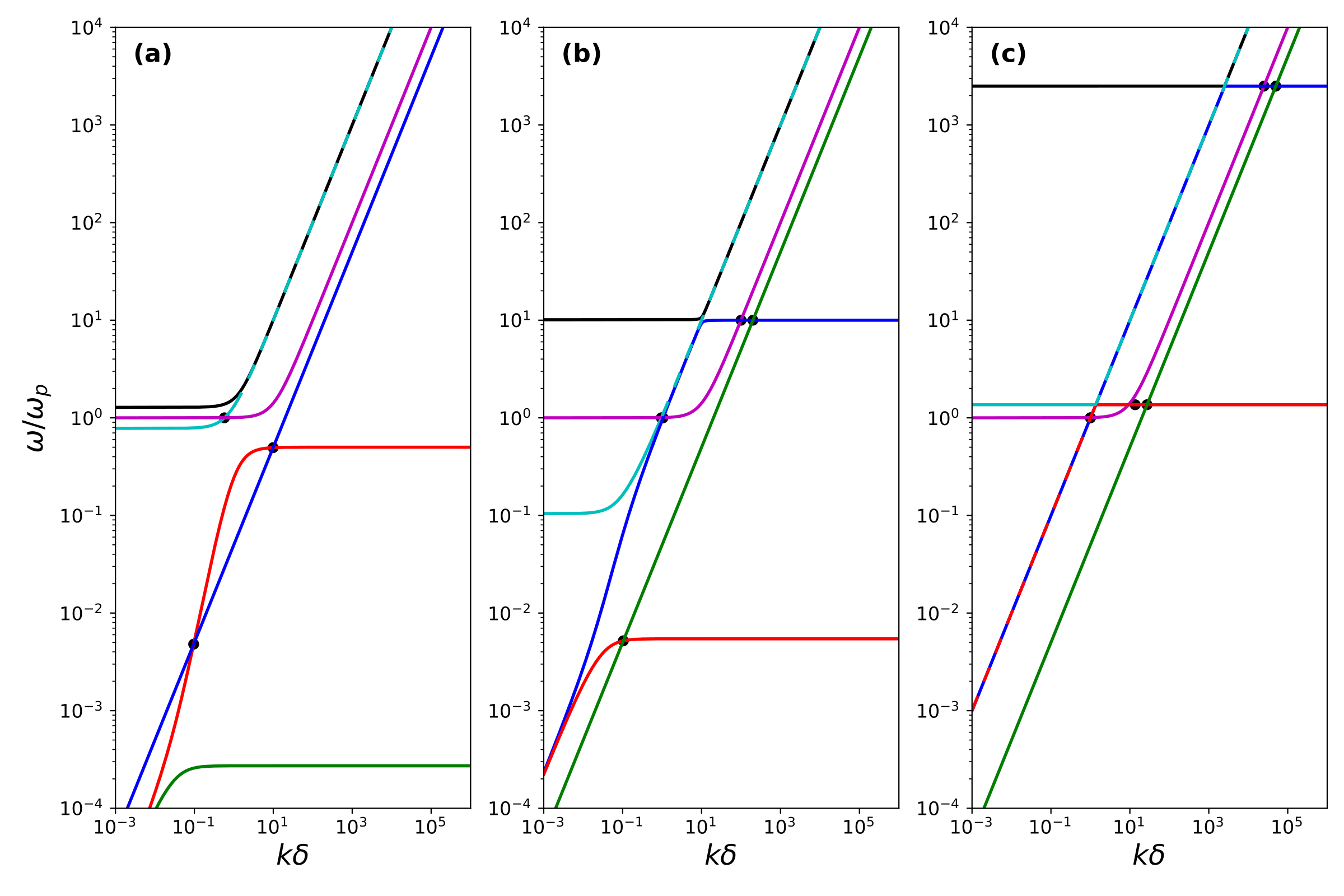
1. Waves in an ion-electron model
The response to inserting small amplitude oscillations in a homogenous background consisting of electrons and one ion species can be described by a dispersion relation that is fully characterised by 5 parameters: the electron and ion magnetisations, the electron and ion sound speeds, and the angle between the propagation vector and the background magnetic field. This dispersion relation features six pairs of forward-backward propagating waves, which we label S (green), A (red), F (blue), M (purple), O (cyan), and X (black). For propagation parallel and perpendicular to the magnetic field modes can cross in the frequency-wavenumber diagram, whilst this is prohibited for oblique angles, thus establishing a mode ordering: S < A < F < M < O < X. The number of mode crossings and which modes cross (at parallel/perpendicular propagation) depends on the parameter regime. We identified 6 parameter regimes at parallel propagation and 2 regimes at perpendicular propagation (where the S and A modes vanish). Below, three different regimes at parallel propagation are shown side by side. Black dots mark analytical approximations of the crossings.
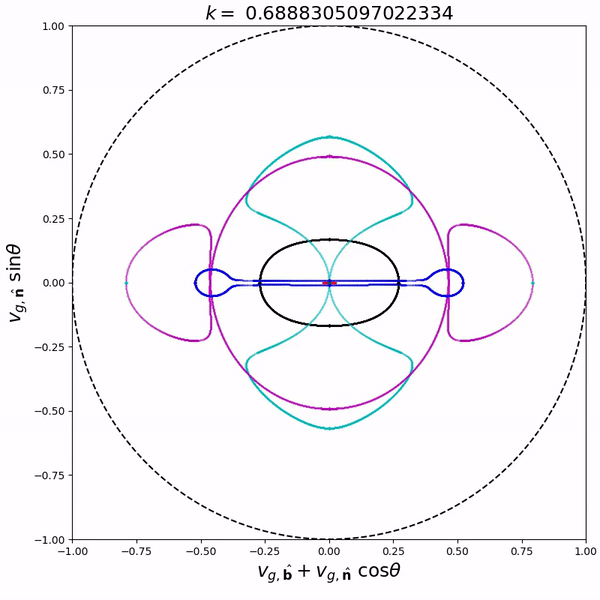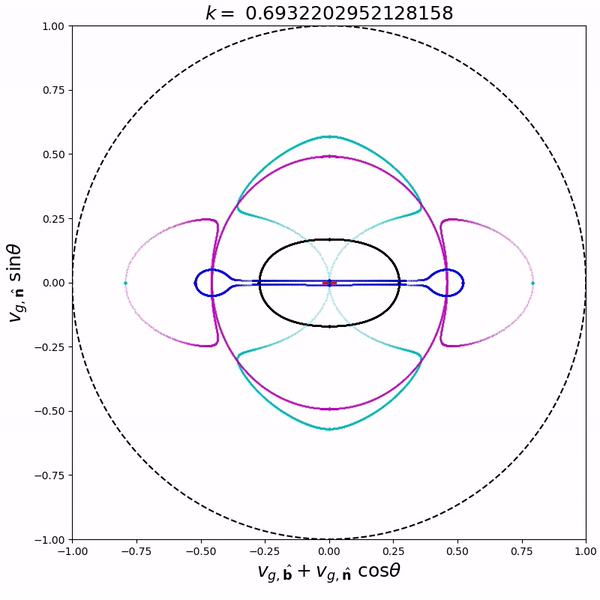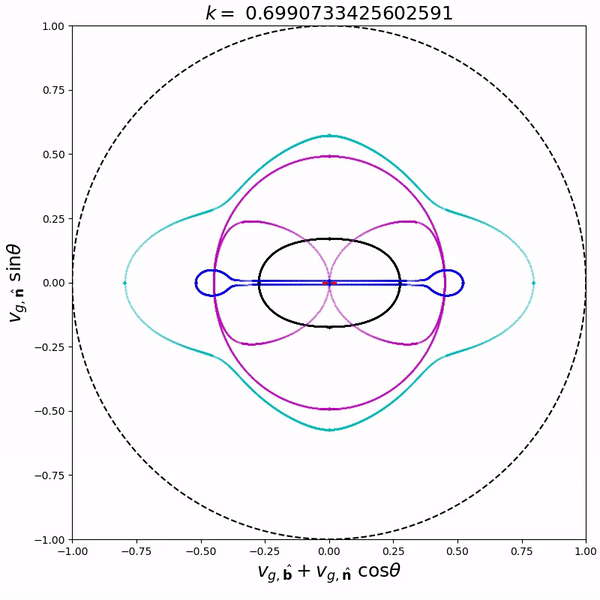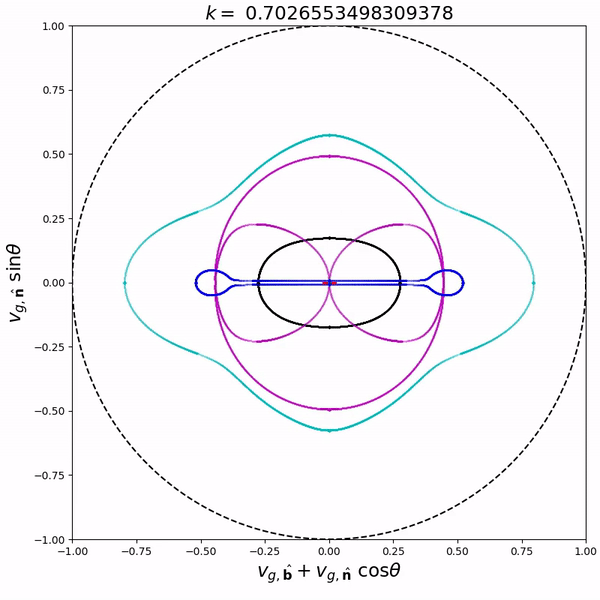
From the dispersion relation, we can also compute the phase and group speed at any propagation angle. Combining the information for all angles in one figure, we get phase and group speed diagrams. On the right is an animated group speed diagram for coronal loop conditions for a wavenumber interval around the avoided MO crossing. As you can see, the group speed curves of the M (purple) and O (cyan) mode reconnect at the avoided crossing. This reconnecting behaviour occurs for all avoided crossings. More diagrams and animations are available in De Jonghe & Keppens (2020) and its supplementary material.
Using the same two-fluid description and group speed expressions, we showed that all six modes exhibit a form of “whistling behaviour”, albeit in different frequency ranges, where the group speed changes drastically with small changes in frequency. Additionally, from this formalism the Appleton-Hartree relation can be derived and expanded to include the effect of the electron thermal velocity. For more information, have a look at De Jonghe & Keppens (2021).
Publications and proceedings
- De Jonghe, J. & Keppens, R. (2020). A two-fluid analysis of waves in a warm ion–electron plasma. Phys. Plasmas 27, 122107. DOI:10.1063/5.0029534. arXiv:2011.06282.
- De Jonghe, J., & Keppens, R. (2021). Two-fluid treatment of whistling behavior and the warm Appleton-Hartree extension. J. Geophys. Res. Space Phys. 126, e2020JA028953. DOI:10.1029/2020JA028953. arXiv:2104.05275.
- De Jonghe, J. & Keppens, R. (2021). Laser-induced Cherenkov radiation in a warm two-fluid model. In 47th EPS Conference on Plasma Physics, EPS 2021, 1235–1238. Link.
- De Vadder, J., De Jonghe, J. and Keppens, R. (2024). “Collisional damping of wave modes in ion-electron plasmas.” J. Plasma Phys. 90(4), 905900410. DOI:10.1017/S0022377824000680. arXiv:2405.11565
2. New physics for Legolas

The development of the Legolas code was initiated by Niels Claes to analyse the influence of non-ideal effects on inhomogeneous plasma configurations in Cartesian or cylindrical geometries. The result is the finite element code Legolas for 1D MHD spectroscopy. When the code became publicly available for the first time, it included flow, resistivity, thermal conduction, radiative cooling, and external gravity. The code and its features are presented in the accompanying release publication Claes, De Jonghe & Keppens (2020), with a variety of test cases from the spectroscopy literature.
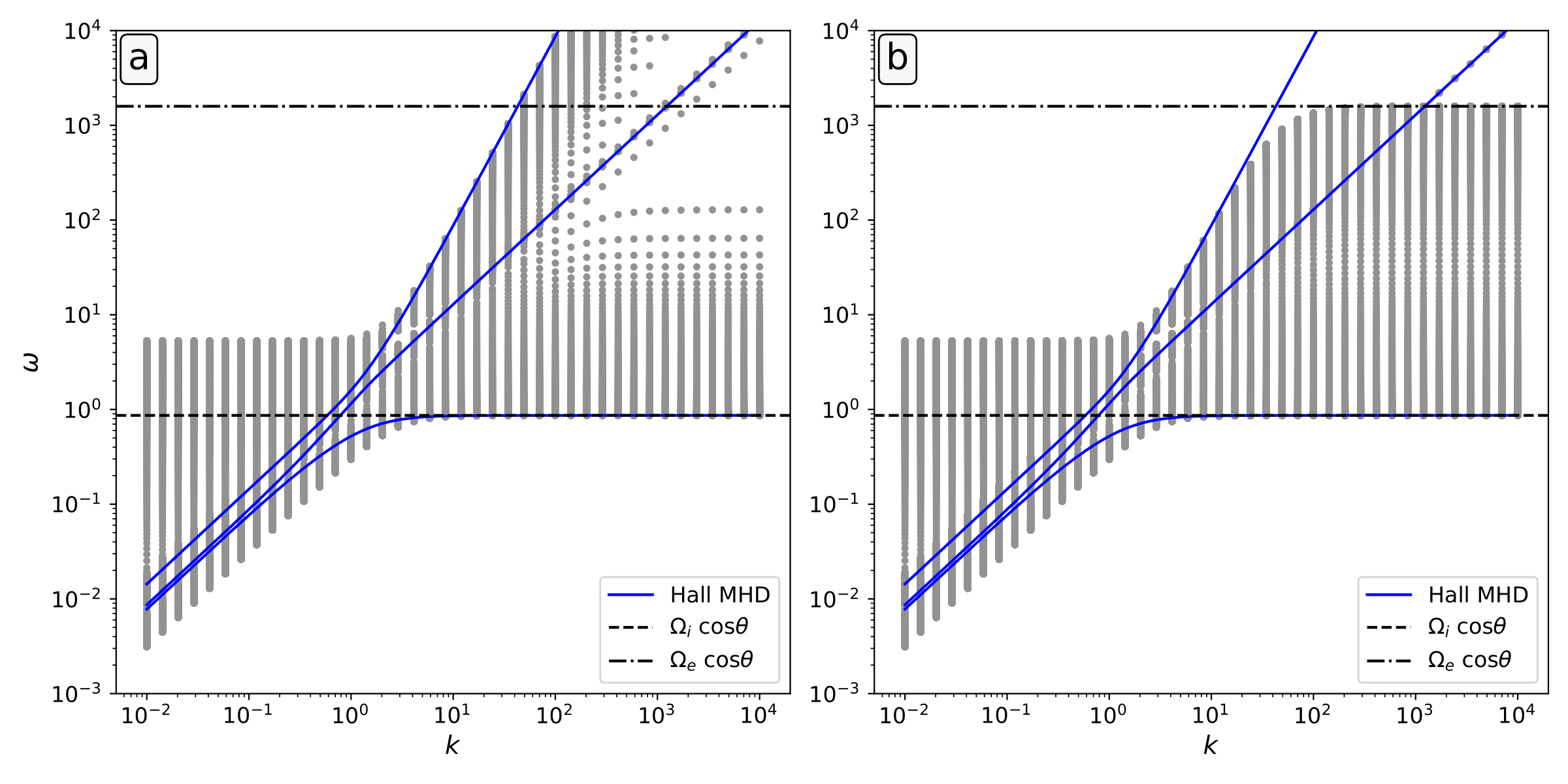
In De Jonghe, Claes & Keppens (2022) we finally present the extension of the code with viscosity and the Hall current, both important effects in evaluating the stability of plasma configurations, e.g. in relation to the resistive tearing mode, alongside other smaller improvements such as the inclusion of an incompressible approximation and calculation of entropy and magnetic field perturbations. Besides viscosity and the Hall current, we also added the option to include the effect of electron inertia. Without the electron inertia term the HMHD model recovers the ion cyclotron resonance, but not the electron cyclotron resonance. Including the electron inertia term also adds the electron cyclotron resonance and brings the HMHD model closer to the two-fluid model. The figure below highlights this with a Legolas multirun of the homogeneous plasma slab with Hall current (a) without electron inertia and (b) with electron inertia term. (The lowest horizontal line is the ion cyclotron resonance, the highest horizontal line is the electron cyclotron resonance, and the blue solid lines are the analytic HMHD solution.) This is just one test case from this paper.
Publications
- Claes, N., De Jonghe, J. & Keppens, R. (2020). Legolas: A modern tool for magnetohydrodynamic spectroscopy. Astrophys. J., Suppl. Ser. 251, 25. DOI:10.3847/1538-4365/abc5c4. arXiv:2010.14148.
- De Jonghe, J., Claes, N. & Keppens, R. (2022). Legolas: Magnetohydrodynamic spectroscopy with viscosity and Hall current. J. Plasma Phys. 88 (3), 905880321. DOI:10.1017/S0022377822000617. arXiv:2206.07377.
3. Tearing instability in flowing media
Ever since its discovery the resistive tearing mode has been the subject of many studies. Interest in this particular instability was recently reinvigorated by its possibly key role in triggering magnetic reconnection, which is required for the violent eruptions witnessed on the solar surface. However, observations are not in line with purely resistive simulations. Hence, other effects are also at play here, and should thus be accounted for. Besides viscosity and the Hall current, which both affect the tearing growth rate, another important candidate presents itself: background flow. Since solar plasma is constantly moving, we seek to understand how the tearing instability is affected by background flow.
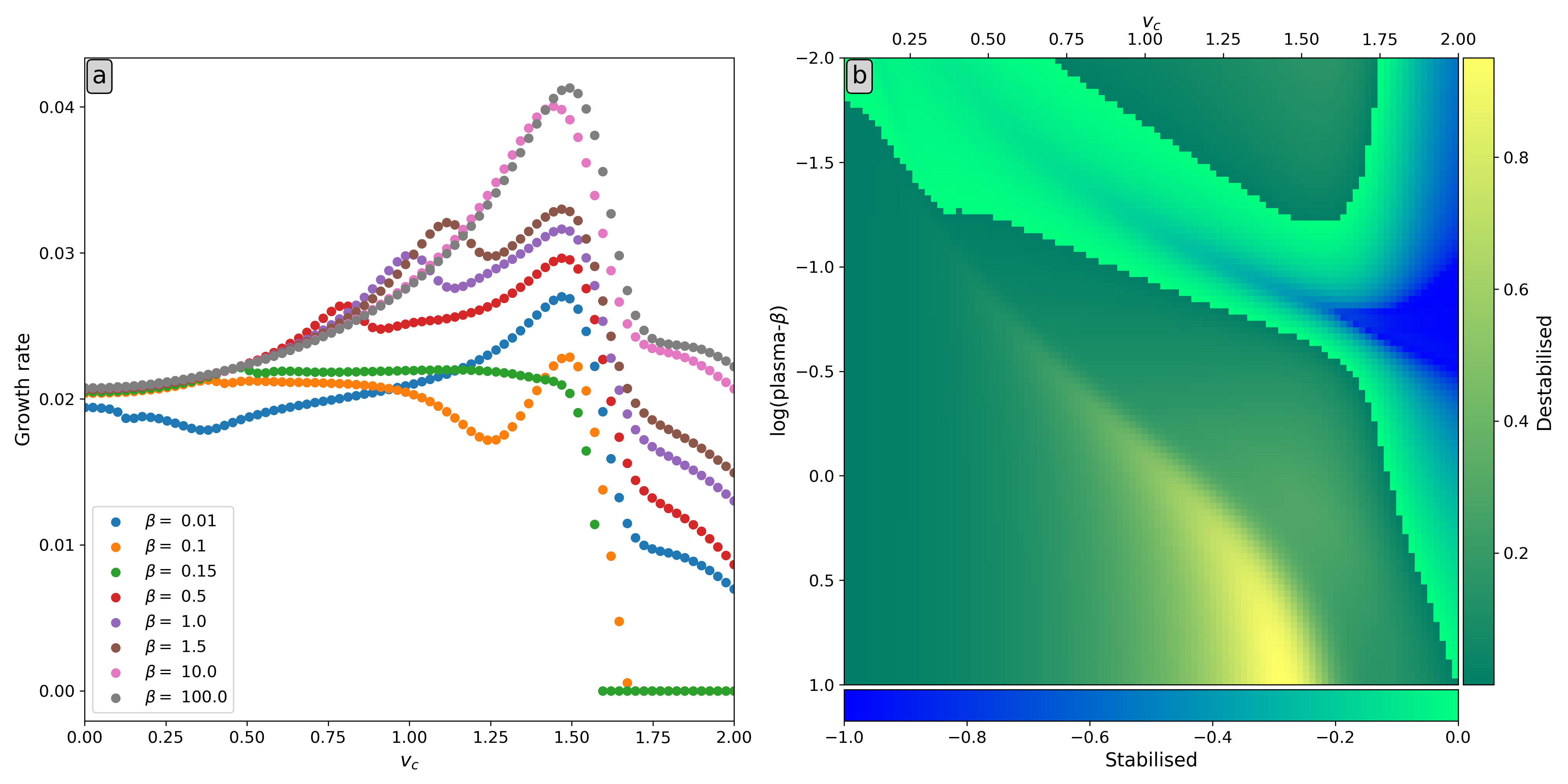
To investigate this issue, we turn to the Legolas multirun framework, which allows us to perform many Legolas runs whilst varying one or more parameters. This can then be done for various setups, such as a magnetic field that varies its orientation throughout a plasma slab or a Harris current sheet, to identify which parameters play a role in the influence of flow on the tearing growth rate. It was found that many parameters affect the growth rate in an intricate way, as evidenced by the image below, showing the tearing growth rate during a simultaneous variation of the velocity coefficient and plasma-$\beta$ for the direction-varying magnetic field case mentioned above. More details and results can be found in the publications listed below.
Publications and proceedings
- De Jonghe, J. & Keppens, R. (2023). Tearing growth rate of a viscoresistive Harris sheet subject to flow. In 49th EPS Conference on Plasma Physics, EPS 2023, O4.201. Link
- De Jonghe, J. and Keppens, R. (2024). “Modification of the resistive tearing instability with Joule heating by shear flow.” Phys. Plasmas. 31(3), 032106. DOI:10.1063/5.0180535. arXiv:2402.12005.
This page was last updated on 10 December 2024.
