
Hi, thank you for your interest in my work!
During my PhD I investigated the influence of optically thin cooling curves and flow on thermal instability. Condensations such as solar prominences in the corona, are formed due to catastrophic energy loss by radiative emission as plasma cools down. This process is called thermal instability. Instead of solving the full radiative transfer equations, precomputed cooling curves are typically used in numerical simulations. In the literature a wide variety of cooling curves exist and they are quite often used as unquestionable ingredients. Flows are omnipresent and govern the dynamics of plasma. Solar tornadoes are a class of apparently rotating prominences, that might be formed by thermal instability. In spectroscopic studies on thermal instability background flow is commonly neglected.
1. Thermal instability and optically thin cooling curves in MHD simulations
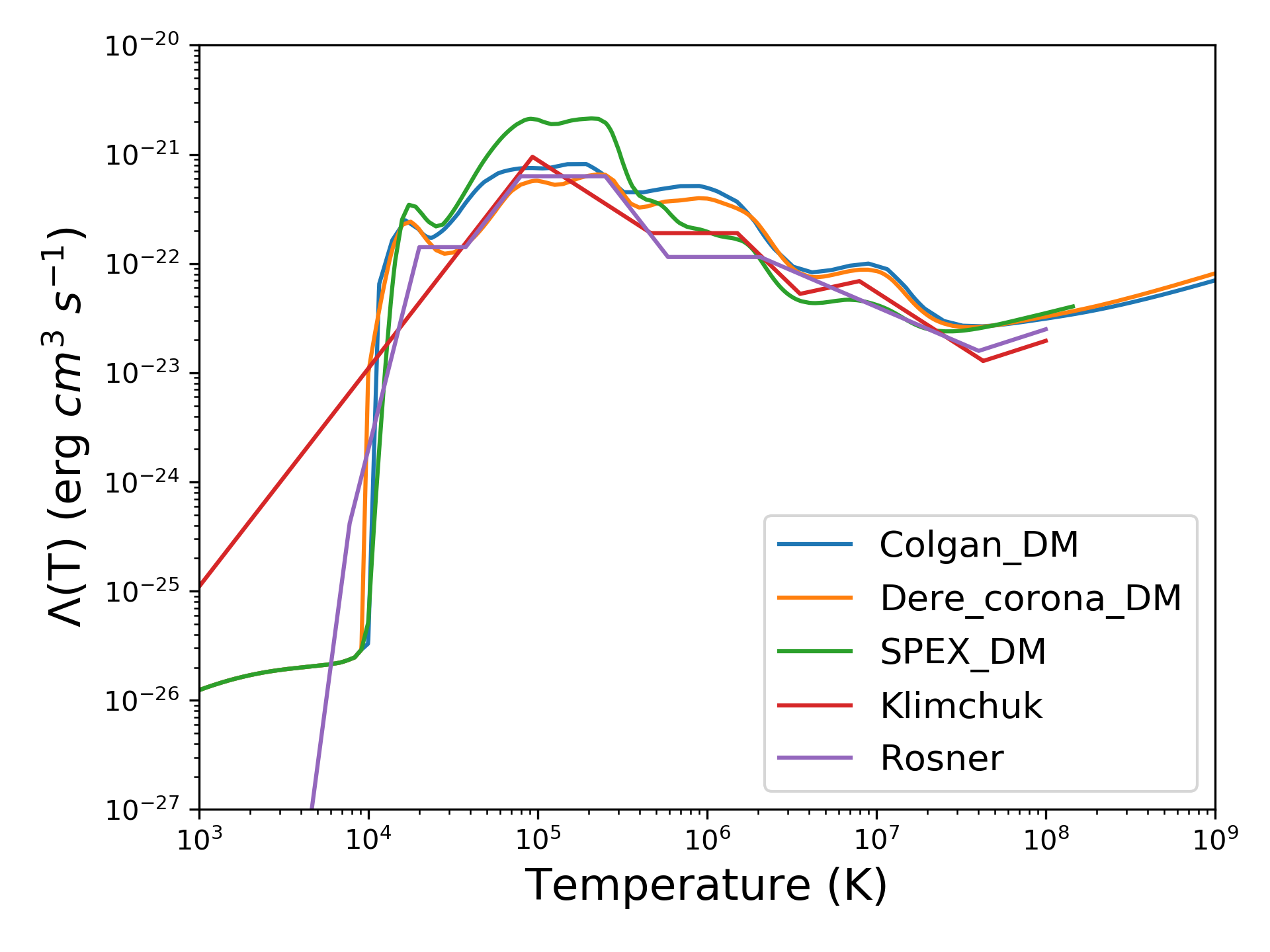
Firstly, we determined the effect of the optically thin cooling curves on the formation and evolution of condensations in numerical simulations. We also investigated the effect of numerical settings. This includes the resolution and the low-temperature treatment of the cooling curves, for which the optically thin approximation is not valid. 2D numerical simulations with different cooling curves were set up using interacting slow magnetohydrodynamic (MHD) waves as trigger for the thermal instability. The five cooling curves that were used are shown on the right. The image below shows snapshots from the five simulations comparing the formation of the condensation. For all tested cooling curves, condensations are formed. The differences due to the change in cooling curve are twofold. First, the growth rate of the thermal instability is different, leading to condensations that form at different times. Second, the morphology of the formed condensation varies widely. Fragmentation of the condensations is affected by the low-temperature treatment of the cooling curves. Condensations formed using cooling curves that vanish for temperatures lower than 20 000 K appear to be more stable against dynamical instabilities. This shows the need for high-resolution simulations as it determines the width and density accumulation of the condensation.
Furthermore, a bootstrap measure was introduced to extend the simulation into the far nonlinear regime of thermal instability. In the nonlinear regime the condensation fragments dynamically align with the background magnetic field. The bootstrap procedure can be used in future multi-dimensional simulations to study fine-structure dynamics in solar prominences. The links to the movies of the benchmark simulation, the extension to the far nonlinear regime, and also an interesting hydrodynamics version are given below.
Based on our results we advocate the use of modern cooling curves, based on accurate computations and current atomic parameters and solar abundances.
Link to movie of benchmark simulation
Link to movie of far nonlinear regime
Link to movie of thermal instability in hydrodynamics

The influence of the numerical implementation of a cooling curve, i.e. piece-wise power law versus interpolated table was also investigated. We therefore created piece-wise power law fits to the SPEX_DM curve (Schure et. al 2009). The analytic formulae for both the fine and rough fits to the SPEX_DM curve are given below.

2. Thermal instability and background flow in MHD spectroscopy

We investigated the effect of background flow on thermal instability using MHD spectroscopy. The non-adiabatic MHD equations were linearised around a cylindrical equilibrium with azimuthal and axial background flow. Assuming wave-like solutions, the equations can be solved to provide the frequencies and eigenfunctions of the eigenmodes of the equilibrium. We extended upon the existing literature by examining the equations analytically and transforming them into two first-order differential equations. The effect of flow on the continua, expressions for which the differential equations become singular, was investigated. The thermal continuum, responsible for the condensation formation, is only Doppler-shifted. The two differential equations do contain additional terms due to the background flow. This will affect discrete modes. Using the eigenvalue code Legolas we verified the analytic results numerically using a benchmark equilibrium with helical magnetic and flow fields based on the well-known Gold-Hoyle equilibrium. A 3D view of the flow field is shown in the figure on the right.
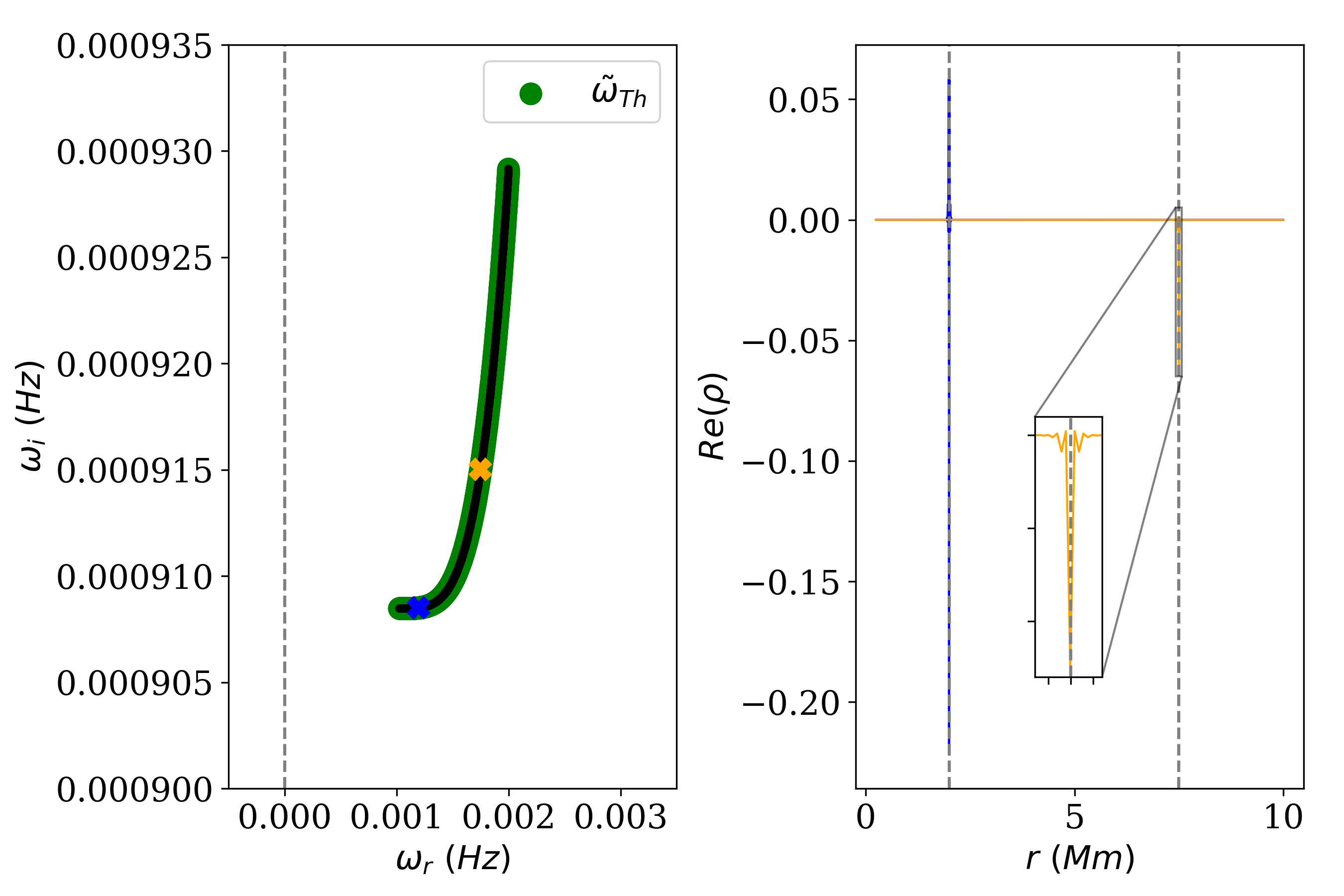
The thermal continuum is plotted in the figure on the left. The green curve represents the analytic expression and matches perfectly with the black dots which are the resutls from Legolas. In the right panel of the figure the hyper-localised eigenfunctions of the thermal continuum modes are shown. A small parametric study was performed. The azimuthal velocity profile, optically thin cooling curve, and wavenumber were varied. The choice of cooling curve influences the location of the most unstable modes, which in turn determines where the in-situ condensation is formed. Furthermore, discrete thermal modes were investigated. An analytic expression to predict the existence of discrete thermal modes based on the equilibrium parameters was derived using a WKB approximation. The expression was also verified using Legolas. We took a look at different equilibria with discrete thermal modes. The eigenfunctions of the discrete modes were visualised in 2D and 3D. From the density distribution and its evolution you can get an indication of how the condensations might look like when observed, as can be seen in the figure below. The 3D image of the streamlines of the total velocity field showed how it is perturbed from a purely helical field by the radial velocity perturbation. The analytic derivations and numerical verifications show that a helical background flow affects thermal instability in various ways.

Outlook
A logical extension to this work is the combination of the two physical processes in multidimensional MHD simulations. The starting point is a ‘simple’ simulation of thermal instability in a local coronal volume, but in 2.5D due to the helicalness of the equilibria. 2.5D simulations would allow for the study of the condensations formed by the continuum and discrete thermal modes at extreme resolutions. Differences to the formed condensations based on the kind of mode might prove useful in understanding observations of prominences and fine-structure. The interplay between the flow and fragmentation of the condensations in the far nonlinear stage is definitely worth investigating. Due to the radial variation of the equilibria used in MHD spectroscopy, physical effects depending on other coordinates are neglected. In the context of prominences and solar tornadoes gravity and the support against it are of the utmost importance. In MHD simulations this can be included and parametric studies can be performed to see what kind of flows and magnetic field configurations are needed to support the prominence mass in helical field. A second important physical improvement is the inclusion of a realistic solar atmosphere with density or temperature stratification. The mentioned physical effects can be included in more demanding 3D simulations, for which the helical shape of the magnetic and flow fields can really flourish and help improve our understanding of solar tornadoes. It must be stressed that the analytic equations derived in this work are valid for more physical environments than solely the solar corona. The solar coronal setup was just used as an example. Thermal instability is a general phenomenon based on energy loss by radiation and flows are present on every scale in the universe. Therefore, there are many more interesting applications, such as the clumpiness of galactic ouflows and three-phase nature of the dynamic interstellar medium.
Publications and proceedings
- Hermans, J. & Keppens, R. (2021). Effect of optically thin cooling curves on condensation formation: Case study using thermal instability. Astronomy & Astrophysics. 655:A36. DOI: 10.1051/0004-6361/202140665. arXiv: 2107.07569.
- Hermans, J. & Keppens, R. (2021). Piece-wise power law or interpolated curve, does it matter for optically thin radiative cooling?. In 47th EPS Conference on Plasma Physics, EPS 2021. Europhysics Conference Abstracts Vol. 45A, pages 381-385. ISBN 9781713837046. Link.
- Hermans, J., & Keppens, R. (2023). A spectroscopic investigation of thermal instability for cylindrical equilibria with background flow. Submitted to Astronomy & Astrophysics
This page was last updated on 8 December 2023.
